За разумевање природе није довољно имати само свакодневно искуство. Елементаријум представља седам уврнутих начина, страних интуицији, размишљања у науци

Текст: Тијана Марковић
Ако погледате свет око себе, нарочито окружење у ком проводите највише времена, рећи ћете да вам је оно потпуно познато. Но, да ли сте се некада запитали шта се крије иза вашег рачунара? Да ли су ствари које посматрате свакодневно баш такве каквим вам се чине? Шта заправо значи да је нешто вероватно 50 одсто? Постоји ли и како изгледа 4Д свет?
Нека од ових питања вас до сада можда никада нису заинтригирала. Друга, пак, делују превише смешно због своје тривијалности и готово свако би на њих одговорио истог тренутка. Међутим, колико сте сигурни да су ти одговори тачни? Смете ли да се кладите у њих?
Када научници покушају да вам понуде и објасне одговоре на оваква питања, може вам се учинити да размишљају на сасвим други начин. И бићете у праву.
За разумевање природе није довољно само имати здрав разум. Неки феномени се не могу схватити на основу свакодневног промишљања. Елементаријум представља седам начина који су страни нашој интуицији, али научници често управо тако размишљају.

1. Како размишљати квантно?
„Свет би постојао без мене, био је ту пре мене и биће ту после мене“, каже Јоханес Кофлер са Института „Макс Планк“ за квантну оптику, из Гархинга у Немачкој.
У квантној механици, честице су описане без потребе да људи постоје и да их виде – описане су вероватносним таласним функцијама. Оно што делује парадоксално јесте што могу бити не само у чистом стању, него и у „суперпозицији“ вишеструких стања и места. У квантној механици постоје и „испреплетане“ честице, које утичу једна на другу и на великим растојањима.
Другим речима, квантни објекти могу бити на више места у исто време, а више њих могу да утичу једни на друге на великим удаљеностима. Како то схватити?
Што се више удубљујете у ову теорију и улазите у њену суштину, примећујете да се она озбиљно сукобљава са вашом интуицијом. Но, човек има проблем да схвати одређене аспекте чак и када је у питању класична реалност. На пример, колико људи би рекло да перје и цигле падају истом брзином под дејством гравитације?
У квантној физици, кванти се користе да објасне објекте који постоје само у математици. Визуализација таласне функције само једне честице природно се може разумети, мада, када се уведу нове честице, те функције прелазе у вишедимензиони простор који готово нико не може да ослика.
Прихватањем квантне физике наилазите на још један сукоб са већ постојећим интуитивним знањима. Пре свега, уласком у квантну механику морате одбацити претпоставку да сваки објекат има утврђене особине, без обзира да ли га мерите или не. Квантни објекти се, наиме, другачије понашају кад их гледате и кад не гледате.
Са друге стране, у квантном свету не важи претпоставка да један објекат не може тренутно да утиче на други.
2. Како одлучивати статистички?
Вероватноћа је једна од ствари око које се увек греши. „Многи ‘чисти’ математичари се жале да у вероватноћи има много нелогичих одговора“, каже Џон Хејг, математичар са Сасекс универзитета у Брајтону, у Великој Британији.
Рецимо да се посматра било која група од 25 ученика. Колика је вероватноћа да међу њима постоји двоје који су рођени истог дана? Интуитивно би већина људи рекла да је шанса за то јако мала, готово једнака нули. Грешка. Веровали или не, вероватноћа овог догађаја је чак око 57 одсто.
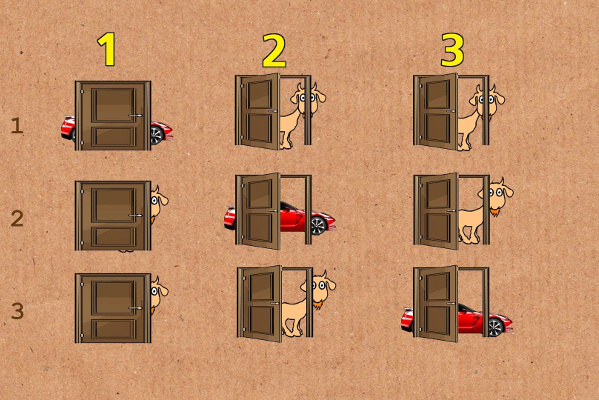
Ако се, пак, бавите Monty Hall проблемом, названим по домаћину америчкког шоуа Let’s Make a Deal, сусрећете се са још једним парадоксом. Замислите да се налазите испред троја врата. Иза једних се крије аутомобил, а иза осталих по коза. Треба да одаберете само једна да бисте добили оно што се иза њих крије.
Након што се одлучите, домаћин, који зна шта се налази иза којих врата, отвара једна иза којих је сигурно коза. Када то учини, ви имате могућност да промените мишљење и отворите трећа, или да останете при првобитном избору, наравно, под претпоставком да тежите освајању кола. Наиван одговор би био да је свеједно која ћете врата изабрати на крају, јер је шанса да погодите где је ауто 50 одсто. Наравно, и ово је погрешан начин размишљања.
Када се бавите вероватноћом, важно је бити свестан једне чињенице, а то је да она није интуитивна. Да би се дошло до исправног решења, прво треба размотрити како је проблем постављен, па тек онда пажљиво рачунати и закључивати на основу познатих чињеница.
Код задатка са рођенданима кључно је приметити да је потребно посматрати парове ученика, а не појединце. Пошто је дато одељење од 25 ђака, могуће је формирати укупно 300 различитих парова, а различитих датума у години има 365 (ако се не узму у обзир преступне године). Након израчунавања добије се решење које износи око 57 одсто.
У Monty Hall задатку вероватноћа да одаберете права врата је 1/3 и она се не мења шта год да се деси потом. Када домаћин покаже козу, шанса да је аутомобил иза других износи 2/3, те је боље да промените избор.

3. Како мислити космолошки?
„Свемир је велики. Стварно велики. Просто не бисте веровали колико је много, огромно, запањујуће велики“, написао је Даглас Адамс у „Аутостоперском водичу кроз галаксију“. Потпуно тачно. Његова „видљива граница“ налази се око неких 46 милијарди светлосних година далеко.
Према теорији великог праска, универзум је настао „ни из чега“ пре око 13,8 милијарди година. Али, како да то разумете на прави начин?
Мартин Рис, космолог на Универзитету Кембриџ сматра да постоје две стратегије за објашњење: угушити себе рачунањем или цртати слике. „Ја бих одабрао свет слика“, каже.
Рис приказује ширећи универзум као чвор на 3Д решетки која се протеже докле ум то може да замисли, а кога са осталим чворовима спајају путеви који се шире. Тако можете визуализовати универзум који се помера од вас у свим правцима. Приметићете да се са сваког чвора може видети иста слика, те је јасно да не постоји централна позиција.
Такође, спољашња граница се и не назире, с обзиром на то да хоризонт не представља нужно и крај нечега. Ван видљивог дела се налазе и многобројне глаксије које се не могу посматрати, јер се превеликом брзином удаљавају од Млечног пута.
Још је изазовније схватити шта је било пре великог праска. Тренутни физички концепти кажу да ово питање нема много смисла јер према њима правац времена не постоји, па нема ни „пре“ ни „после“ нечега.

4. Како говорити математички?
„Математика је као језик – али онај, који захваљујући својој уграђеној логици пише сам себе“, сматра математичар Иан Стјуарт. „Можете почети да записујете ствари не знајући тачно шта оне представљају, али језик ће вам дати потребне сугестије.“ Они који савладају математичке основе врло брзо могу да уђу у њену суштину. Међутим, зашто већина мисли да се овом науком могу бавити само телентовани?
Алекс Белос, математичар и писац, тврди да је један од разлога због чега људи не разумеју математику, недостатак времена. „Претпоставка није да све треба да буде једноставно.“
Сликовито приказивање може помоћи и у овом случају. Узмите као пример негативне бројеве. Пет оваца је једноставно избројити, али шта са минус пет? „Њих је немогуће замислити, па је бесмислено мучити се таквим стварима“, са овом изјавом се доста људи слаже. Слично је и са комплексним, дводимензионалним бројевима који описују математику квантне теорије.
Аналогија доста помаже у неким ситуацијама. Ако вам је мучно да размишљате о елипси, замислите спљоштен круг и радите са њим.
Супротно мишљењу о математици као дисциплини снажне логике, најбољи начин да нападнете проблем било које врсте је да направите кратак резиме о њему, прескочите оно са чиме не можете да баратате, касније се вратите назад и допуните детаље. Једну ствар треба увек имати у виду, при решавању математичких проблема, корисно је размишљати нејасно.
5. Како посматрати релативистички?
Простор и време зависе од тога одакле се мере. Два посматрача са батеријским лампама путују брзим возовима. Сваки од њих може да тврди да је први укључио своју лампу и да притом буде у праву, посматрано са његове тачке гледишта.
Астронаути који се налазе на Међународној свемирској станици (International Space Station – ISS) старе мало спорије због брзине којом се крећу и мало брже, услед слабијег деловања гравитације на Земљи. Ипак, ефекти се не поништавају. Брзина побеђује у овој трци, доприносећи томе да астронаут који проведе шест месеци на ISS-ју bude 0,007 секунди млађи од некога ко је остао на матичној планети.
Релативност зато може да буде пуна парадокса. Да би се спречиле такве несугласице, прво треба да пажљиво размислите о томе како ваше кретање утиче на вашу перцепцију протицања времена других људи. Мада, исто тако треба мислити како и други могу да другачије виде пролажење вашег времена.
Син Карол, физичар са Калифорнијског института за технологију у Пасадени, има неколико правила којих се придржава услед образовања своје слике о реалности. „У основи, време је нешто као простор, али не потпуно исто. Главна разлика је у томе што су у простору најкраћа растојања између две тачке праве линије, док су у времену оне најдуже.“
Ако одлетите негде брзином светлости, затим се вратите назад, имаћете осећај да је прошло мање времена, за разлику од оног ко је све време седео. Време пролази спорије када се забављате.

6. Како мислити у више димензија?
Физичар Кaрло Ровели, професор на Институту у Марсеју, нема проблема што се тиче прихватања постојања виших димензија. Он тврди да је кључна ствар у њиховом прихватању правилно размишљање: „То је само простор у коме можете ићи горе и доле, лево и десно, напред и назад, али и у још једној димензији, лево2 и десно2. Као да имамо много руку, попут индијског бога.“
Међутим, други научници су обазривији што се тиче овог проблема. Један од начина лежи у разумевању, пре свега нижих димензија, па тек онда разматрању виших.
Тај процес је у роману Равница описао Едвин Абот 1884. године, а гласи: Када 3Д Сфера пролази кроз 2Д Равницу становници дводимензионалне плоче је виде као тренуту тачку која расте у велики круг, пре пре него што се трансформише назад у тачку.“
Ипак, како је посматрање објеката у више од три димензије још немогуће, окретање ка математици представља одличан корак. Решење сада постаје једноставније јер је само потребно, на већ постојеће Декартове координате x, y и z, додати нове, на пример, u, w, t,… итд. За сада, овај модел савршено функционише, наравно, под претпоставком да више димензије заиста постоји.

7. Како разумети рачунарски?
Рачунари примају информације које обрађују по претходно задатим алгоритмима, производећи одређене излазне податке. Ако посматрате живот биљака које користе угљен-диоксид за фотосинтезу и тако производе кисеоник, приметићете да и оне функционишу као прави рачунар. Размишљајући о томе, вероватно можете пронаћи још много примера „живих“ рачунара.
Међутим, овим путем основни појам речи речи „рачунар“ знатно мења значење. Један од начина да се то избегне је хијерархијско посматрање машина.
Први у низу су аутомати, попут семафора или лифтова, који раде нешто више од пролажења кроз ограничену серију улазних и излазних података.
Затим следе дигитални, односно Тјурингови рачунари. Сви рачунари какве познајемо данас развијени су по идеји Алана Тјуринга о универзалној машини. Она ради на принципу учитавања инструкција преко веома дуге улазне траке, а прави су показатељи недостатака, односно ограничености, рачунара.
Ипак, постоје одређени проблеми које ниједан рачунар не може да реши. На питање „Да ли ће се овај програм зауставити?“, добићете одговор само након покретања истог.
Текст је настао на основу темата How to think about, објављеног у научнопопуларном часопису New Scientists у броју 2999. Истражите више кроз рубрику THINKLIST…
