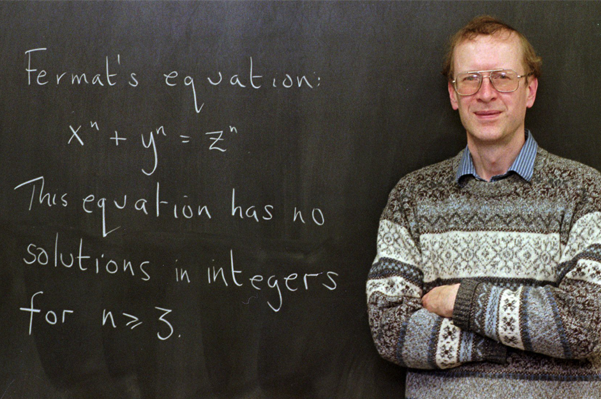Endrju Vajls dobitnik je prestižnog priznanja Abel za dokaz teoreme koja je godinama važila za najteži matematički problem
Tekst: Jovana Nikolić
Kako je saopšteno 15. marta, ovogodišnji dobitnik prestižne Abelove nagrade je Endrju Vajls, čiji je dokaz Fermaove teoreme Norveška akademija nauka nazvala epohalnim trenutkom za matematiku. Put do dokaza teoreme, koja je godinama u Ginisovoj knjizi rekorda bila označena kao najteži matematički problem, bio je dug 358 godina.
Francuski matematičar i pravnik Pjer de Ferma je 1637. godine proučavajući Diofantov spis ”Aritmetika” iz trećeg veka ostavio jednu belešku koja će zadati velike teškoće brojnim matematičarima koji su pokušali da otkriju šta je to Ferma znao a sačuvao samo za sebe.
Kako Ferma nije bio sklon objavljivanju svojih radova, njegov sin nakon očeve smrti kreće u potragu za pismima, radovima i spisima iz kojih se može saznati više o njegovom radu, pa čak uzima u obzir i beleške koje je ostavljao u knjigama. Tako pronalazi na marginama ”Aritmetike” opis čuvene jednačine na latinskom jeziku uz reči da je dokaz veličanstven ali da nema dovoljno prostora za njegovo izvođenje na belini ove knjige.
Fermaova poslednja teorema glasi: ne postoje tri različita pozitivna cela broja za koje važi jednačina an +bn= cn ako je n veće od 2.
Dok postavka ove teoreme deluje veoma jednostavno, dokaz je toliko komplikovan da je veći deo vremena od njenog nastanka prošao u uverenju matematičara da se ova teorema ne može dokazati. Među poznatim matematičarima bilo je ne samo onih koji su joj se divili i nazivali je najinteresantnijom teoremom, već i onih koji su je smatrali šaljivom besmislicom.
Iako je teoremu bilo moguće dokazati za neke cele brojeve, teoremu je bilo gotovo nemoguće dokazati u opštem slučaju. Sam Ferma je dokazao da je teorema istinita za n koje ima vrednost 4, a brojni matematičari su dokazali za neke druge brojeve među kojima su se, sa razvojem kompjutera, našli čak i sedmocifreni. Ipak, dokaza za sve brojeve nije bilo.
Potraga za njim je obeležena brojnim pokušajima, rivalstvima ali i jednom neobičnom anegdotom. Krajem 19. veka nemački industrijalac i matematičar amater Pol Volfsekhl je isplanirao svoje samoubistvo tačno odredivši njegov trenutak. Međutim, Fermaova teorema je toliko zaokupila njegovu pažnju da nije primetio kada je sat otkucao ponoć a kasnije je odsutao od svoje namere i odlučio da nagradu vrednu današnjih 2 miliona dolara ponudi onome ko dokaže ”teoremu koja mu je spasila život”. Ova ponuda je učinila da stigne više od 600 dokaza, ali nijedan dobar.
Sa neobičnom teoremom, čija se formula danas pominje u brojnim naučnofantastičnim romanima i popularnim filmovima i serijama, Endrju Vajls se susreo u lokalnoj biblioteci kada je imao samo 10 godina. Čitajući knjigu ”Poslednji problem” Erika Templa Bela, poptuno ga je oduševilo saznanje da postoje nerešeni problemi koji na prvi pogled deluju toliko jasno da o njima može da razmišlja čak i desetogodišnjak. Naredne godine obeležila je Vajlsova neuspešna potraga za dokazom, a nakon što je postao profesor na Univerzitetu Prinston, provodi sedam godina na jednom tavanu u svojoj kancelariji, pokušavajući da u tajnosti dođe do rešenja.
Vajls je dokaz izveo na indirektan način polazeći od Tanijamine pretpostavke koja govori o eliptičkim krivama. Kenet Ribet i Gerhard Frej su dokazali da istinitost ove pretpostavke povlači istinitost Fermaove teoreme. U junu 1993. godine, Endrju Vajls je konačno bio spreman da svoja saznanja iznese javno što je i učinio na tri uzastopna predavanja na Univerzitetu u Kembridžu.
Dok je ispisivao na tabli dokaz najzagonetnije teoreme, u sali je sedelo oko 200 matematičara od kojih je mali broj mogao u potpunosti da isprati čitav postupak. Ipak, zavladalo je potpuno oduševljenje.
Međutim, dva meseca kasnije, Vajls dobija informaciju da je u njegovom dokazu pronađena greška i narednu godinu provodi ispravljajući je zajedno sa Ričardom Tejlorom. Dokaz napisan na više od 150 strana konačno je objaveljen 1995. godine, a 21 godinu kasnije doneo je Vajlsu Abelovu nagradu.
Endrju Vajls je dokazao Fermaovu teoremu na način koji zahteva čitavo jedno polje matematike, koje je bilo nepoznato u 17. veku. Sledeće pitanje za matematičare jeste – kako je Ferma dokazao ovu teoremu. Postoje samo tri mogućnosti. Teorema se može dokazati na drugačiji način pomoću znanja koja su bila dostupna, Ferma je znao metode za koje se smatra da su tek kasnije otkrivene ili je svojom beleškom želeo samo da se našali.