Da li je telo koje je nedavno napravio Kreg Kaplan samo razonoda ili još jedna potvrda da aproksimacije doprinse preciznosti?

Tekst: Slađana Šimrak
Kanađanin Kreg Kaplan, profesor računarstva, nedavno je na svom blogu postavio fotografiju tela koje je konstruisano od kartona. Bio je to poliedar sastavljen od četiri pravilna dvanaestougla i dvanaest pravilnih desetouglova. Pri sklapanju su se pojavile šupljine koje takođe nisu bile proizvoljne već oblika jednakostraničnih trouglova, ukupno njih dvadeset osam. Pažljivim posmatračima ovo izgleda kao savršeno telo, ali postoji jedna začkoljica: ono zapravo ne postoji.
Pravilni mnogouglovi i tela koja od njih nastaju su, zahvaljujući svojoj lepoti i konstrukcijskim izazovima, zanimali matematičare još od Pitagore, a nešto kasnije i Euklida, koji im je posvetio čak dve knjige svojih Elemenata. Pre pedesetak godina matematičari su sve moguće konveksne poliedre čije su strane pravilni mnogouglovi rasporedili u pet grupa: Platonova tela, Arhimedova tela, Džonsonova tela, prizme i antiprizme. I još su dokazali da ne postoji nijedno telo koje zadovoljava ove kriterijume a da ne pripada nijednoj grupi.
Međutim, poliedar koji je Kaplan sastavio, zaista nije član nijedne. Ono nije izuzetak već je samo približno „savršeno”. Autor je pravio male aproksimacije stranica i uglova, a potom seckao viškove kako bi dobio ovo telo koje se tek za dlaku razlikuje od potpuno pravilnog. Bez merenja razlika se ne vidi pa ono izgleda kao novi član Džonsonove grupe poliedara. Zanimljiva popodnevna igra. Međutim, zašto je ovakvo razmišljanje matematički važno? Može li dovesti do većih naučnih rezultata? Kakve mogućnosti krije „približno” u haosu teorijske preciznosti?

Kvadratić koji nedostaje
Bertrand Rasel piše: „Iako ovo zvuči paradoksalno, u svakoj preciznoj nauci dominira ideja aproksimacije. Kada vam neko kaže tačnu istinu o nečemu, slobodni ste da zaključite da je on neprecizan čovek”. Ovakvim temama igrali su se čak i mađioničari. Jedan amater po imenu Pol Kari je 1953. godine sastavio igru koja se zvala „Nedostajući kvadrat”.
Radilo se o pravouglom trouglu na kvadratnoj mreži sastavljenom od jasno oivičenih delova. Razmeštanjem tih delova u novi poredak dolazilo se do novog trougla koji je izgledao isto kao početni ali njegova površina bila je umanjena za jedan kvadratić. Trik se sastojao u tome da je hipotenuza početnog trougla bila aproksimirana krivom, a razlika između te krive i prave hipotenuze drugog trougla bila je jednaka površini pomenutog kvadratića. Ova igra i danas okupira pažnju.
Upravo na aproksimacijama, procenama i nefizičkim pretpostavkama leži evolucija nauke. Rast populacije nije tačno eksponencijalna funkcija. Nijedan krug sastavljen od atoma nema odnos obima i prečnika u vrednosti π. Istovremeno, znati približnu vrednost broja π ne znači gotovo ništa ukoliko ne stoji zajedno sa znanjem kako je ova aproksimacija dovela do novih naučnih saznanja. Arhimedova „metoda iscrpljivanja” koja je dovodila do preciznijih aproksimacija broja π dala je temelj razvoju integralnog računa.
Kada je Kopernik pokazao da je Sunce centar oko kojeg se kreću planete, svi su pretpostavljali da se one kreću po kružnoj putanji konstantnom brzinom. Johan Kepler nije podržavao ovu ideju zato što se nije uklapala u postojeće podatke u vezi sa Marsovom putanjom. Tako je pokazao da ove podatke zadovoljavaju elpise. Znao je da je elipsa aproksimacija kruga ako su žiže dovoljno blizu, pa je jednostavno stavio Sunce u jednu od žiža elipse i tako je nastao prvi Keplerov zakon.
Međutim, nije bio zadovoljan rezultatima u potpunosti pa je došao i do zaključka da se brzina kretanja planete menja tokom obilaska oko Sunca. Rezultat je bio drugi Keplerov zakon. Ovi radovi, objavljeni 1609. godine, predstavljali su veliki naučni podvig i jedan su od važnijih istorijskih primera kako se od ograničenih podataka i pogodnih aproksimacija mogu dobiti zapanjujući rezultati.
Da Vinčijev mnogougao
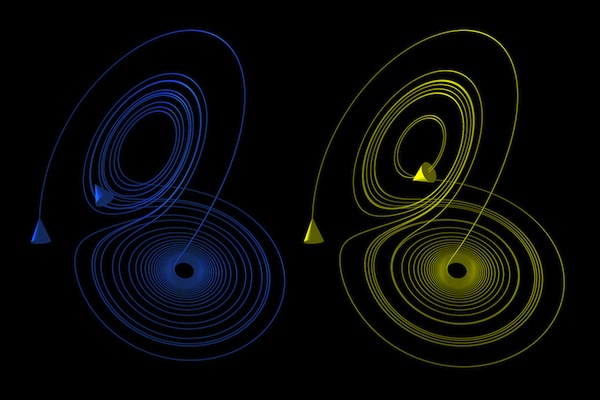
Jedan od naučnika koji je aproksimacijom otvorio novo poglavlje u skorijoj istoriji matematike bio je Edvard Norton Lorenc. Ovaj američki matematičar poznat je po uvođenju pojmova „efekat leptira” i „čudni atraktori” u nauku. Takođe je dokazao da vremenska prognoza ne može da se predvidi u prihvatljivoj tačnosti za period duži od dve nedelje. Njegovi matematički modeli sastavljeni od tri jednačine sa tri nepoznate pokazali su da postoje ograničenja u predviđanjima za određene determinističke sisteme. Ovo sjajno zapažanje, koje kaže da moramo da prihvatimo približna predviđanja kada je reč o velikim dinamičkim sistemima poput atmosfere, dovelo je do rađanja nove naučne oblasti pod imenom „teorija haosa”, koja se posle teorije relativnosti i kvantne mehanike smatra trećom naučnom revolucijom dvadesetog veka.
Greška aproksimacije je uporediva sa greškom fizičkih elemenata kao što su olovka, papir i ruka, pa su aproksimativne metode za efikasnije crtanje komplikovanih tela bile naročito interesantne umetnicima. Kada je starogrčka matematika doživela ponovno rođenje u Evropi tokom renesanse, umetnici sa matematičkim sklonostima preusmerili su svoja interesovanja na istraživanja problema perspektive i bavljenja neizostavnim zlatnim presekom.
Kako je on često povezan sa pravilnim mnogouglovima, tragali su za modelima konstrukcije ovih figura. Nije bilo važno da li su metode stare ili nove i bilo je dovoljno da skice budu približne. Leonardo da Vinči, iako nije bio metodičan pisac, s vremena na vreme zapisao bi po neku metodu za crtanje pravilnih mnogouglova. Mada je Euklid dao tačnu metodu za konstruisanje petougla, da Vinči je došao do veoma preciznog aproksimativnog načina. Sličan uspeh imao je i Albreht Direr dajući tačnu metodu za konstrukciju pravilnih mnogouglova, ali i jednu za približno crtanje koja je naročito bila korisna zanatlijama i zidarima. Direrova sistematička pitanja o ovoj temi učinila su da on više nego da Vinči sačuva popularne srednjovekovne konstrukcije za buduća proučavanja.
