Saznanje da ipak postoje iracionalni brojevi podelilo je jednu filozofsku družinu
Pitagorejci, družina filozofa koju je u 6. veku p.n.e. osnovao Pitagora iz Samosa, otkrili su mnogo značajnih matematičkih pravila i raširili ih među starim Grcima. Kasnije su veliki filozofi poput Platona i Aristotela prihvatili i objasnili mnoga pitagorejska učenja.
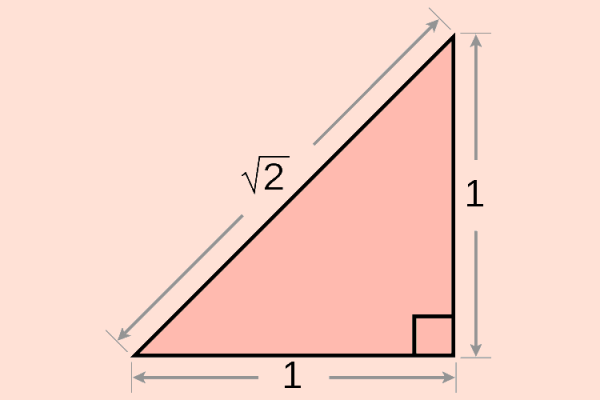
Međutim, kao što je i osnovano, društvo pitagorejaca se raspalo zbog brojeva. Jedan od članova ove grupe, Hipas iz Metaponta, pokušavao je da izračuna dužinu dijagonale u kvadratu stranice 1, ali je ustanovio da ona ne može da se predstavi odnosom dva prirodna broja. Matematičari danas znaju da je ta dužina jednaka √2, korenu iz broja 2, što je iracionalan broj koji ne može da se predstavi razlomkom.

Hipasovo otkriće je užasnulo pitagorejce koji su verovali da sve stvari, a među njima i dužina jedne dijagonale, sigurno mogu da se predstave prirodnim brojevima. Neki pitagorjci su izvršili samoubistvo posle ovog saznanja. Ostali su počeli da se svađaju među sobom i društvo se potom raspalo na dva dela.
Danas je poznato da brojevi mogu biti racionalni i iracionalni, već prema tome da li mogu ili ne mogu da se zapišu razlomkom. Najpoznatiji iracionalan broj je √2, ali je takav i √3, kao i mnogi drugi.
Najzanimljiviji iracionalan broj je takozvani Ludolfov broj, poznatiji kao π, Pi, čija se vrednost 3,1415926535897932384626433832795…. zapisuje beskonačnim nizom cifara, ali se najčešće koristi samo kao 3,14. Isprva korišćen samo za izračunavanje obima kruga pomoću prečnika (O=R π), Pi je postao nezamenjiv u modernoj nauci kao konstanta koja se nalazi u većini formula matematike i fizike.
 BROJEVI
BROJEVI
Centar za promociju nauke organizuje nacionalnu naučnopopularnu manifestaciju Maj mesec matematike koja će matematiku izvesti na ulice, trgove, galerije i druge javne prostore. Tim povodom, Elementarijum donosi seriju priča o brojevima.
Istražite Malu školu matematike.
Istražite kreativni atlas velikih matematičarki.
