Уочи предавања које ће Џејмс Тентон одржати 25. маја у 18 часова, Елементаријум објављује један његов узбудљив есеј у преводу Александре Равас

Текст: Џејмс Тентон
Превела: Александра Равас
Моја каријера математичара и наставника математике почела је када сам имао 10 година. Наравно да у то време нисам то схватао, али кад сад размишљам о томе, јасно ми је као дан да је моје путовање кроз богати свет математичке игре – а користим реч игра са озбиљном намером – почело захваљујући плафону старе куће грађене у викторијанском стилу који је био обложен плочама од пресованог лима.
Одрастао сам у Аделејду, у Аустралији, у кући која је изграђена почетком 20. века. Плафон сваке од соба имао је своју геометријску шару, и ја сам сваке ноћи у својој соби тонуо у сан зурећи у квадратну мрежу димензија 5×5 која се налазила на плафону. (Линије квадратне мреже биле су назначене виновом лозом, а у сваком ћошку налазио се цветни орнамент).

Пребројавао сам квадрате и правоугаонике у шари. Замишљао сам путеве кроз појединачне квадрате и дуж граничних линија. Покушавао сам и да сместим неке фигуре које нису биле квадрати у пресечне тачке мреже. Укратко, тонућу у сан, на тој квадратној мрежи играо сам читав низ игара и решавао загонетке, а све сам их сам измишљао. Известан број тих загонетки које су посебно занимљиве и дубоке, све ове године врзма ми се по глави:
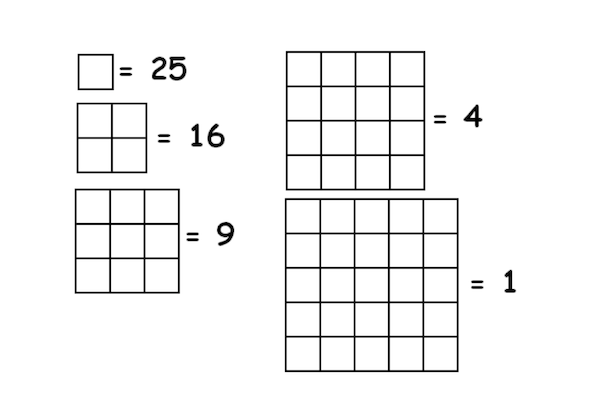
1. Преброј колико квадрата различитих величина постоји у мрежи димензија 5×5. Да ли је очигледно да је сваки тај број потпуни квадрат?
2. Ако се крене од горњег левог угла и ако се могу правити само хоризонтални и вертикални кораци, да ли је могуће проћи путем који би тачно једном прешао преко сваког квадрата у мрежи:
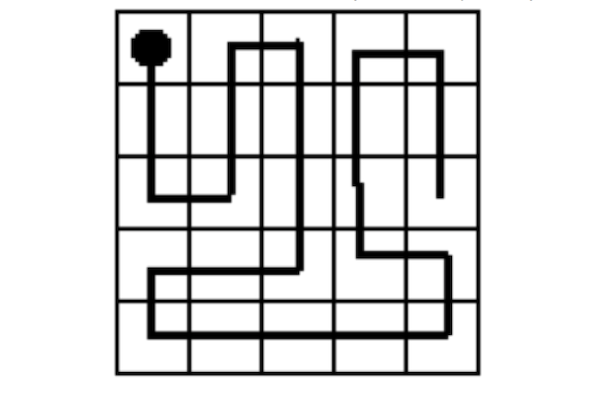
Да ли је могуће започети такав пут из било ког изабраног квадрата у мрежи? Постоји неки проблем у вези са трећом сликом која следи.
3. Да ли је могуће упарити суседне квадрате у мрежи тако да онај у средини преостане као ”прекобројан”?
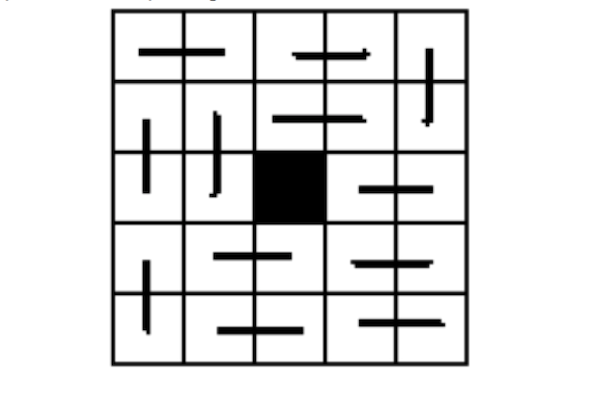
Да ли квадрат који се налази у једном од ћошкова може да постане прекобројан? Да ли сваки квадрат у мрежи може да се издвоји на наведени начин?
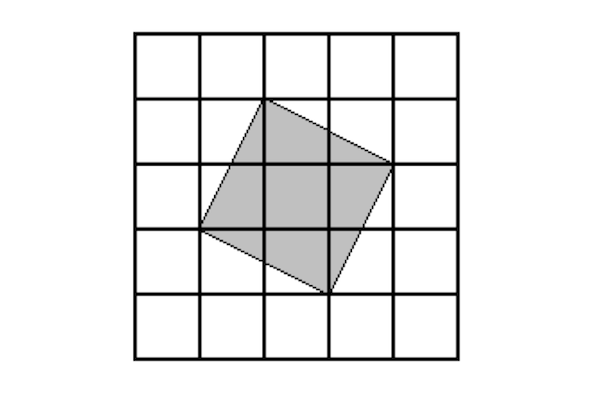
4. Колико се укупно квадрата може наћи у мрежи ако се броје и искошени квадрати попут овог који је приказан на слици?
5. Да ли је могуће нацртати у мрежи једнакокраки троугао коме ће темена бити у њеним пресечним тачкама? А једнакостраничан троугао? Да ли би се у троугаоном низу тачака могао нацртати квадрат?
Понекад се питам да ли сам можда био необично дете – али ипак сматрам да нисам. Природа игре – то јест, интелектуално истраживање, интелектуална радозналост, тежња за знањем – урођена је у нашем истинском бићу. Деца свих узраста уживају у откривању правилности и уживају у истеривању тих правилности до крајњих граница. (Погледајте! 1=1, 1+3=4, 1+3+5=9, 1+3+5+7=16, 1+3+5+7+9=25, квадратни бројеви! Изгледа да је збир непарних бројева потпуни квадрат. Да ли то значи да је збир првих милион непарних бројева једнак квадрату милиона?)
Потрага за правилностима чини срж науке и научног истраживања, па самим тим и математике. Али, математичари инсистирају на томе да се ствари одведу корак даље што истражују и трагају за логичким објашњењима и дубоким разумевањем. Да ли постоји било који разлог да верујемо да је нека конкретна правилност истинита? (Да ли је збир првих n непарних бројева заиста увек једнак n2 ? Како можемо да будемо сигурни да је заиста тако?) Математичари уживају и у доказивању чињенице да су правилности валидне, али и у проналажењу примера у случајевима када правилности не постоје.
Са формалним изучавањем математике почињемо у основној школи отркивајући радост у области аритметике. Спознајемо природне бројеве и основне операције које можемо извршити са њима. Нека деца, на пример, уживају у израчунавању квадрата и кубова бројева, или примете да множење два броја која се завршавају цифром 6 за резултат даје број који се такође завршава цифром 6, или да не постоји потпуни квадрат који се завршава цифром 8. На самом почетку школовања, од нас се често тражи да уочимо правилности и, уколико нам је наставни план занимљив и просвећен, можда ће нам тражити да покушамо да објаснимо зашто нека правилност важи.
Међутим, често се у стандардном учењу математике у неком тренутку дешава да се ствари промене. Време које је било посвећивано истраживању у игри са идејама користи се за стицање низа потребних вештина и компетенција. Сећам се како сам у петом разреду поставио питање наставнику зашто је производ два негативна броја позитиван и како је једини одговор који сам добио био да ту чињеницу треба да прихватим као истину и да пређем на решавање задатака који су ми били при руци. Још као дете научио сам да је моја улога на овом следећем нивоу математичког образовања пасивна, и да не треба да постављам питања.
Али једном сам то поновио, и драго ми је да сам то урадио. Сматрам да је то моје друго животно искуство које ме је одредило као будућег математичара. На часу посвећеном Питагориној теореми, наставник је тражио од ђака у разреду – свих нас тридесет петоро – да нацртамо по три правоугла троугла у свеци, измеримо дужине страница, доделимо им слова a, b и c (Наравно! Постоје ли неки други симболи за ово?) и да изведемо одговарајућу рачуницу како бисмо показали да ли важи да је ”a на квадрат плус b на квадрат једнако c на квадрат”.
Сећам се како су сви остали урадили задатак слажући се да је то био случај у сваком урађеном примеру и да због тога сигурно мора да важи и у општем случају (?). Ја нисам био убеђен и подигао сам руку да питам: ”Како знамо да ово није само случајност? Можда смо имали среће 102 пута за редом”. (Постојао је и други проблем који ми је пао на памет, а који нисам изговорио, наиме ја уопште нисам поверовао да је било ко добио да та једнакост важи чак и на једном примеру: дужине се не могу прецизно измерити!) Наставников одговор је био дирљив. Рекао је: ”Врати се и нацртај још три правоугла троугла”. Крај расправе! Моја сумња била је потврђена: Уколико сам желео да откријем зашто би Питагорина теорема могла да важи, морао сам да се ослоним на сопствене снаге. Провео сам неколико следећих година свог живота (на махове) покушавајући да откријем зашто би она требало да важи.
Да будем искрен, лично сматрам да је средњошколска математика поприлично неинспиративна и ограничавајућа. Моја жеља да постављам питања, истражујем идеје, суочавам се са питањима зашто, и да се интелектуално играм, иако није била угашена, чекала је нека боља времена. И тек када сам почео да слушам универзитетски курс из апстрактне алгебре и теорије бројева – курс који је, у суштини, једноставно постављао питање ”зашто” у оквирима средњошколске аритметике – открио сам свој инстински интелектуални дом и игралиште. У неком смислу, моје интелектуално биће постало је слободно. Било је то радосно и ослобађајуће искуство.
Али, чак и на факултету имао сам утисак да сам изузетак: већина мојих колега жалила се да је курс превише апстрактан, превише далеко од ”стварног света”, лишен смисла и једноставно претежак. Није ми било јасно. Зар моје колеге нису напокон могле да увиде да је овај један курс нудио објашњења зашто је већина ствари коју смо учили у оквиру аритметике и алгебри у школи била тачна? Зар сад нису могли да увиде зашто је растављање броја на чиниоце увек давало исти резултат? Зашто производ два негативна броја једноставно мора да буде позитиван? Зашто комплексни бројеви имају смисла и помажу у решавању стварних проблема? Зашто је Паскалов троугао повезан са ослобађањем од заграда при множењу полинома? Тај курс није очекивао од нас да откривамо правилности и будемо тиме задовољни, већ је објашњавао зашто правилности и запажања морају да је важе. То је била права математика!
Након овог присећања – а можда ћу бити превише строг – питам се да ли су неке од мојих колега осетиле да су превише на губитку када се постави питање чему да верују а чему да не верују. Сећам се да сам више него једном чуо питање ”зашто морамо да доказујемо нешто за шта већ знамо да важи?”. ”Учили” су нас до тада да су многе чињенице ”очигледне”: уколико је неки број дељив са 2 и дељив са 3, онда очигледно, тај број мора бити и дељив са 6! (Дакле исто важи и за бројеве 6, 8 и њихов производ 48?) Дељење са разломцима је, наравно, само множење њиховим реципрочним вредностима (?). Ручно дељење бројева са потписивањем једноставно ради!
Можда су моје колеге биле принуђене да прихвате изнете чињенице без постављања питања – управо онако како сам и ја некад мислио да треба – и можда су од тада на сигурном интелектуалном терену па им је најлакше да им се каже шта је у математици истинито. Одговор на питање ”зашто морамо да доказујемо нешто за шта већ знамо да важи?” гласи: зато што, за почетак, нико од нас лично не зна да је то тачно!
У среду, 25. маја, Џејмс Тентон ће одржати предавање у великом амфитеатру Хемијског факултета у Београду. Предавање Playing with Math: Figurate Numbers and the Square Root of Two почиње у 18 часова, а на њему ће Тентон квадратне и троугаоне бројеве представити кроз историју међународних стандардних величина папира. Истражите више…
Ова едиција једноставно има за циљ да поново испита стандардни наставни план и програм математике за основне и средње школе, почевши од аритметике и алгебре, и настављајући даље, како би се омогућило уживање у сласти интелектуалне игре, а да се то ни не примети. Да ли је нула паран или непаран број? Зашто је 30 = 1 а 0=1!? Зашто правило за дељивост бројем 3 уопште ради? Како гласи правило за дељивост бројем 7? Зашто је производ два негатвина броја позитиван? Шта све можемо сазнати из Паскаловог троугла? Да ли треба да верујемо у правилности? Шта је бесконачност? Шта је тачно ”Хорнерова шема” и шта се ту у ствари дешава? Да ли постоји основа један и по? Колико има простих бројева? Зашто су прости бројеви занимљиви? Хајде да све то откријемо!
Ова књига препуна је истраживачких задатака (истовремено и ”конкретних” и ”мисаоних”) који су редом замишљени да од свакога измаме и проширивање постојећих и постављање нових питања. Успех у истраживању, било оно научно или пословно, резултат је постављања питања, истраживања и играња са идејама, флексибилности размишљања и иновативности углова посматрања. Наравно, наставници могу и треба да науче ђаке читавом низу вештина – а то је важан и сврсисходан задатак. Али, то не треба да буде крај приче.
Ми наставници не би требало да ускраћујемо ђацима могућност да истражују креативни аспект који положај математичара носи са собом. Међутим, то подразумева да ми сами морамо да разумемо тај креативни процес. Надам се да ће ове књиге бити од помоћи у том смислу. Желимо да негујемо иновацију, увиђање и флексибилност размишљања. Желимо да подигнемо на виши ниво истински лично разумевање и жељу за постизањем дубине сопственог знања. И сасвим сигурно, желимо да учење математике доноси богатство и радост. Типичн средњошкослки наставни план и програм енглеског језика учи ђаке и граматици и поезији. Наставни план и програм математике треба да ради исто.
Додуше, ове књиге подразумевају да је читалац – актуелни наставник, будући наставник, ђак, родитељ, или било ко заинтересован за математику – већ имао додира са добрим делом типичног школског програма математике. Књиге се заснивају на тој претпоставци, а избор оваквог приступа није био случајан из неколико разлога.
1. Дубина личног разумевања само је резултат враћања на неку причу више пута. Када се започне са новом темом, велики део менталних напора потроши се на разумевање технологије, самих идеја и осећаја за њу. Процес прилагођавања сопстевног размишљања новим идејам и новим приступима може бити узбудљив, али и фрустрирајући. Међутим, сама чињеница да је неко прочитао на пример, поглавље о логаритмима, и одрадио предвиђена вежбања из њега, и може да ”уради” задатке који се тичу наведене теме, обично не значи да је тај неко усвојио тему и стигао до нивоа њеног потпуног разумевања. Сама дубина теме може се сагледати тек онда када смо се навикли на топографске одлике њене површине. Како је један од циљева овог текста да укаже на дубину сваке од тема које се изучавају, морамо бити спремни да је истражимо.
2. Књига је написана са циљем да помогне развој и јачање личног разумевања математике, али и да помогне онима који су укључени у процес да праве боље и оправдане изборе својих предавачких метода и приступа ученицима. Иако детаљи сваког конкретног наставног плана и програма варирају од школе до школе и зависе од уџбеника који се користи (па последично није могуће директно се наслонити на све постојеће наставне планове и програме) изабрали смо да у овој едицији следимо стандардне обимне наставне теме. Из тог разлога, ове књиге би требало сматрати неком врстом прегледа прича о аритметици, алгебри, функцијама, интегралном и диференцијалном рачуну, вероватноћи, статистици итд. на начин на који су оне приказане у школи.
Не нудимо савете нити препоруке како предавати конкретну тему (упркос чињеници да се током читања овог текста може изродити мноштво специфичних наставних идеја). Циљ је једноставно да помогнемо наставнику или родитељу да развије и ојача своје сопствено разумевање, да буде довољно обавештен како би могао да доноси личне педагошке изборе, и да научи како да изађе на крај са питањима која постављају ђаци. Ученици који буду читали књиге, откриће дубину материјала које су изучавали у школи, али и добре назнаке како размишља један математичар. Све у свему, циљ ове књиге је да познате концепте одведе на нове и узбудљиве нивое.
3. Лако је, релативно лако ”радити” математику. Али, иновативност и иницијатива захтевају отклон од обичног ”решавања” задатака ка креативном и инвентивном. Водећа компанија настоји да помера границе, да ствара и поставља нова питања, да трага за новим идејама и да проналази нове погледе на познате ствари. Научно истраживање делује са истим циљем. Како се предаје вештина постављања питања? Усмеравње пажње на детаље конкретног наставног плана, иако је важно, можда не помогне у решавању проблема опште перспективе. У овој едицији изабрали смо да нагласимо широке теме како бисмо илустровали ”перспективу” и да понудимо контекст и начин на који се могу истражити узбудљиви интелектуални домени – чак и у оквиру нечег познатог.
4. Још један циљ ове едиције је да једноставно прикаже ментални склоп активног математичара, да укаже на лепоту математике, и да омогући уживање у чистој радости истраживања овог чудесног предмета. Пошто је већ искусио велики део стандардног наставног програма школске математике, читалац поседује кутију са алатом којим ће се играти. Опремљени смо за игру!
Зато…, хајде да почнемо са решавањем! Без обзира на начин који будете изабрали да читате ову књигу – пажљиво читајући и мозгајући од почетка до краја, или прелиставајући је и заустављајући се на стварчицама које вам упадну у очи – надам се да ћете имати богато, интригантно, просветљујуће, корисно и понајвише радосно искуство, јер учење математике и бављење математиком управо треба да буде радосно! Граматика и поезија у исто време.
Аутор текста је Џејмс Тентон, познати математичар и овогодишњи гост Маја месеца математике. Истражите више о Тентоновом гостовању у Београду
