Uoči predavanja koje će Džejms Tenton održati 25. maja u 18 časova, Elementarijum objavljuje jedan njegov uzbudljiv esej u prevodu Aleksandre Ravas

Tekst: Džejms Tenton
Prevela: Aleksandra Ravas
Moja karijera matematičara i nastavnika matematike počela je kada sam imao 10 godina. Naravno da u to vreme nisam to shvatao, ali kad sad razmišljam o tome, jasno mi je kao dan da je moje putovanje kroz bogati svet matematičke igre – a koristim reč igra sa ozbiljnom namerom – počelo zahvaljujući plafonu stare kuće građene u viktorijanskom stilu koji je bio obložen pločama od presovanog lima.
Odrastao sam u Adelejdu, u Australiji, u kući koja je izgrađena početkom 20. veka. Plafon svake od soba imao je svoju geometrijsku šaru, i ja sam svake noći u svojoj sobi tonuo u san zureći u kvadratnu mrežu dimenzija 5×5 koja se nalazila na plafonu. (Linije kvadratne mreže bile su naznačene vinovom lozom, a u svakom ćošku nalazio se cvetni ornament).

Prebrojavao sam kvadrate i pravougaonike u šari. Zamišljao sam puteve kroz pojedinačne kvadrate i duž graničnih linija. Pokušavao sam i da smestim neke figure koje nisu bile kvadrati u presečne tačke mreže. Ukratko, tonuću u san, na toj kvadratnoj mreži igrao sam čitav niz igara i rešavao zagonetke, a sve sam ih sam izmišljao. Izvestan broj tih zagonetki koje su posebno zanimljive i duboke, sve ove godine vrzma mi se po glavi:
1. Prebroj koliko kvadrata različitih veličina postoji u mreži dimenzija 5×5. Da li je očigledno da je svaki taj broj potpuni kvadrat?
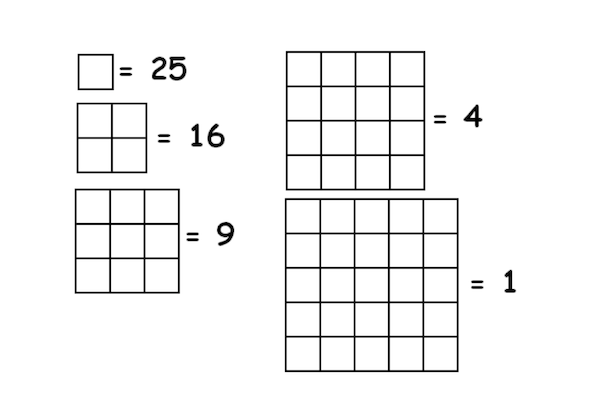
2. Ako se krene od gornjeg levog ugla i ako se mogu praviti samo horizontalni i vertikalni koraci, da li je moguće proći putem koji bi tačno jednom prešao preko svakog kvadrata u mreži:
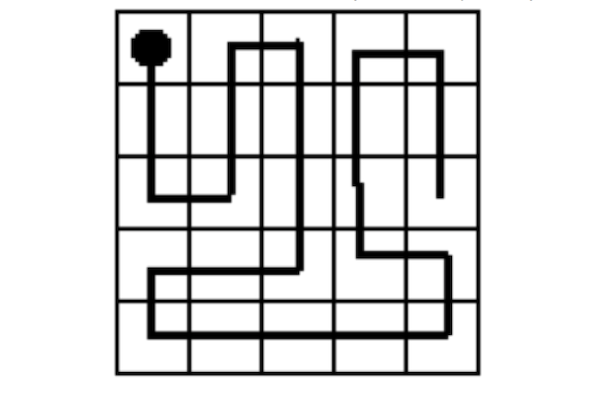
Da li je moguće započeti takav put iz bilo kog izabranog kvadrata u mreži? Postoji neki problem u vezi sa trećom slikom koja sledi.
3. Da li je moguće upariti susedne kvadrate u mreži tako da onaj u sredini preostane kao ”prekobrojan”?
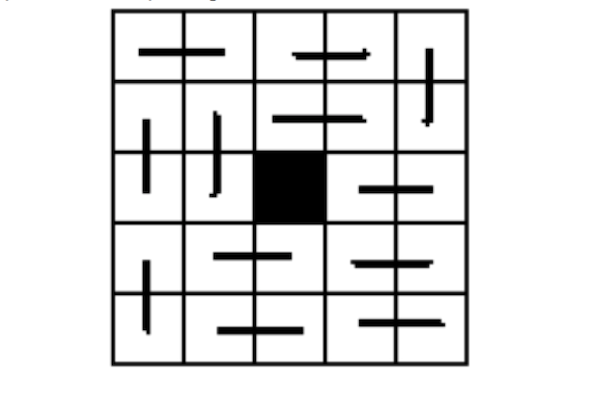
Da li kvadrat koji se nalazi u jednom od ćoškova može da postane prekobrojan? Da li svaki kvadrat u mreži može da se izdvoji na navedeni način?
4. Koliko se ukupno kvadrata može naći u mreži ako se broje i iskošeni kvadrati poput ovog koji je prikazan na slici?
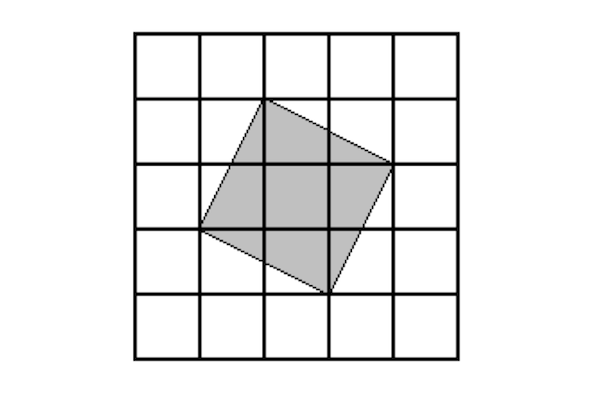
5. Da li je moguće nacrtati u mreži jednakokraki trougao kome će temena biti u njenim presečnim tačkama? A jednakostraničan trougao? Da li bi se u trougaonom nizu tačaka mogao nacrtati kvadrat?
Ponekad se pitam da li sam možda bio neobično dete – ali ipak smatram da nisam. Priroda igre – to jest, intelektualno istraživanje, intelektualna radoznalost, težnja za znanjem – urođena je u našem istinskom biću. Deca svih uzrasta uživaju u otkrivanju pravilnosti i uživaju u isterivanju tih pravilnosti do krajnjih granica. (Pogledajte! 1=1, 1+3=4, 1+3+5=9, 1+3+5+7=16, 1+3+5+7+9=25, kvadratni brojevi! Izgleda da je zbir neparnih brojeva potpuni kvadrat. Da li to znači da je zbir prvih milion neparnih brojeva jednak kvadratu miliona?)
Potraga za pravilnostima čini srž nauke i naučnog istraživanja, pa samim tim i matematike. Ali, matematičari insistiraju na tome da se stvari odvedu korak dalje što istražuju i tragaju za logičkim objašnjenjima i dubokim razumevanjem. Da li postoji bilo koji razlog da verujemo da je neka konkretna pravilnost istinita? (Da li je zbir prvih n neparnih brojeva zaista uvek jednak n2 ? Kako možemo da budemo sigurni da je zaista tako?) Matematičari uživaju i u dokazivanju činjenice da su pravilnosti validne, ali i u pronalaženju primera u slučajevima kada pravilnosti ne postoje.
Sa formalnim izučavanjem matematike počinjemo u osnovnoj školi otrkivajući radost u oblasti aritmetike. Spoznajemo prirodne brojeve i osnovne operacije koje možemo izvršiti sa njima. Neka deca, na primer, uživaju u izračunavanju kvadrata i kubova brojeva, ili primete da množenje dva broja koja se završavaju cifrom 6 za rezultat daje broj koji se takođe završava cifrom 6, ili da ne postoji potpuni kvadrat koji se završava cifrom 8. Na samom početku školovanja, od nas se često traži da uočimo pravilnosti i, ukoliko nam je nastavni plan zanimljiv i prosvećen, možda će nam tražiti da pokušamo da objasnimo zašto neka pravilnost važi.
Međutim, često se u standardnom učenju matematike u nekom trenutku dešava da se stvari promene. Vreme koje je bilo posvećivano istraživanju u igri sa idejama koristi se za sticanje niza potrebnih veština i kompetencija. Sećam se kako sam u petom razredu postavio pitanje nastavniku zašto je proizvod dva negativna broja pozitivan i kako je jedini odgovor koji sam dobio bio da tu činjenicu treba da prihvatim kao istinu i da pređem na rešavanje zadataka koji su mi bili pri ruci. Još kao dete naučio sam da je moja uloga na ovom sledećem nivou matematičkog obrazovanja pasivna, i da ne treba da postavljam pitanja.
Ali jednom sam to ponovio, i drago mi je da sam to uradio. Smatram da je to moje drugo životno iskustvo koje me je odredilo kao budućeg matematičara. Na času posvećenom Pitagorinoj teoremi, nastavnik je tražio od đaka u razredu – svih nas trideset petoro – da nacrtamo po tri pravougla trougla u sveci, izmerimo dužine stranica, dodelimo im slova a, b i c (Naravno! Postoje li neki drugi simboli za ovo?) i da izvedemo odgovarajuću računicu kako bismo pokazali da li važi da je ”a na kvadrat plus b na kvadrat jednako c na kvadrat”.
Sećam se kako su svi ostali uradili zadatak slažući se da je to bio slučaj u svakom urađenom primeru i da zbog toga sigurno mora da važi i u opštem slučaju (?). Ja nisam bio ubeđen i podigao sam ruku da pitam: ”Kako znamo da ovo nije samo slučajnost? Možda smo imali sreće 102 puta za redom”. (Postojao je i drugi problem koji mi je pao na pamet, a koji nisam izgovorio, naime ja uopšte nisam poverovao da je bilo ko dobio da ta jednakost važi čak i na jednom primeru: dužine se ne mogu precizno izmeriti!) Nastavnikov odgovor je bio dirljiv. Rekao je: ”Vrati se i nacrtaj još tri pravougla trougla”. Kraj rasprave! Moja sumnja bila je potvrđena: Ukoliko sam želeo da otkrijem zašto bi Pitagorina teorema mogla da važi, morao sam da se oslonim na sopstvene snage. Proveo sam nekoliko sledećih godina svog života (na mahove) pokušavajući da otkrijem zašto bi ona trebalo da važi.
Da budem iskren, lično smatram da je srednjoškolska matematika poprilično neinspirativna i ograničavajuća. Moja želja da postavljam pitanja, istražujem ideje, suočavam se sa pitanjima zašto, i da se intelektualno igram, iako nije bila ugašena, čekala je neka bolja vremena. I tek kada sam počeo da slušam univerzitetski kurs iz apstraktne algebre i teorije brojeva – kurs koji je, u suštini, jednostavno postavljao pitanje ”zašto” u okvirima srednjoškolske aritmetike – otkrio sam svoj instinski intelektualni dom i igralište. U nekom smislu, moje intelektualno biće postalo je slobodno. Bilo je to radosno i oslobađajuće iskustvo.
Ali, čak i na fakultetu imao sam utisak da sam izuzetak: većina mojih kolega žalila se da je kurs previše apstraktan, previše daleko od ”stvarnog sveta”, lišen smisla i jednostavno pretežak. Nije mi bilo jasno. Zar moje kolege nisu napokon mogle da uvide da je ovaj jedan kurs nudio objašnjenja zašto je većina stvari koju smo učili u okviru aritmetike i algebri u školi bila tačna? Zar sad nisu mogli da uvide zašto je rastavljanje broja na činioce uvek davalo isti rezultat? Zašto proizvod dva negativna broja jednostavno mora da bude pozitivan? Zašto kompleksni brojevi imaju smisla i pomažu u rešavanju stvarnih problema? Zašto je Paskalov trougao povezan sa oslobađanjem od zagrada pri množenju polinoma? Taj kurs nije očekivao od nas da otkrivamo pravilnosti i budemo time zadovoljni, već je objašnjavao zašto pravilnosti i zapažanja moraju da je važe. To je bila prava matematika!
Nakon ovog prisećanja – a možda ću biti previše strog – pitam se da li su neke od mojih kolega osetile da su previše na gubitku kada se postavi pitanje čemu da veruju a čemu da ne veruju. Sećam se da sam više nego jednom čuo pitanje ”zašto moramo da dokazujemo nešto za šta već znamo da važi?”. ”Učili” su nas do tada da su mnoge činjenice ”očigledne”: ukoliko je neki broj deljiv sa 2 i deljiv sa 3, onda očigledno, taj broj mora biti i deljiv sa 6! (Dakle isto važi i za brojeve 6, 8 i njihov proizvod 48?) Deljenje sa razlomcima je, naravno, samo množenje njihovim recipročnim vrednostima (?). Ručno deljenje brojeva sa potpisivanjem jednostavno radi!
Možda su moje kolege bile prinuđene da prihvate iznete činjenice bez postavljanja pitanja – upravo onako kako sam i ja nekad mislio da treba – i možda su od tada na sigurnom intelektualnom terenu pa im je najlakše da im se kaže šta je u matematici istinito. Odgovor na pitanje ”zašto moramo da dokazujemo nešto za šta već znamo da važi?” glasi: zato što, za početak, niko od nas lično ne zna da je to tačno!
U sredu, 25. maja, Džejms Tenton će održati predavanje u velikom amfiteatru Hemijskog fakulteta u Beogradu. Predavanje Playing with Math: Figurate Numbers and the Square Root of Two počinje u 18 časova, a na njemu će Tenton kvadratne i trougaone brojeve predstaviti kroz istoriju međunarodnih standardnih veličina papira. Istražite više…
Ova edicija jednostavno ima za cilj da ponovo ispita standardni nastavni plan i program matematike za osnovne i srednje škole, počevši od aritmetike i algebre, i nastavljajući dalje, kako bi se omogućilo uživanje u slasti intelektualne igre, a da se to ni ne primeti. Da li je nula paran ili neparan broj? Zašto je 30 = 1 a 0=1!? Zašto pravilo za deljivost brojem 3 uopšte radi? Kako glasi pravilo za deljivost brojem 7? Zašto je proizvod dva negatvina broja pozitivan? Šta sve možemo saznati iz Paskalovog trougla? Da li treba da verujemo u pravilnosti? Šta je beskonačnost? Šta je tačno ”Hornerova šema” i šta se tu u stvari dešava? Da li postoji osnova jedan i po? Koliko ima prostih brojeva? Zašto su prosti brojevi zanimljivi? Hajde da sve to otkrijemo!
Ova knjiga prepuna je istraživačkih zadataka (istovremeno i ”konkretnih” i ”misaonih”) koji su redom zamišljeni da od svakoga izmame i proširivanje postojećih i postavljanje novih pitanja. Uspeh u istraživanju, bilo ono naučno ili poslovno, rezultat je postavljanja pitanja, istraživanja i igranja sa idejama, fleksibilnosti razmišljanja i inovativnosti uglova posmatranja. Naravno, nastavnici mogu i treba da nauče đake čitavom nizu veština – a to je važan i svrsishodan zadatak. Ali, to ne treba da bude kraj priče.
Mi nastavnici ne bi trebalo da uskraćujemo đacima mogućnost da istražuju kreativni aspekt koji položaj matematičara nosi sa sobom. Međutim, to podrazumeva da mi sami moramo da razumemo taj kreativni proces. Nadam se da će ove knjige biti od pomoći u tom smislu. Želimo da negujemo inovaciju, uviđanje i fleksibilnost razmišljanja. Želimo da podignemo na viši nivo istinski lično razumevanje i želju za postizanjem dubine sopstvenog znanja. I sasvim sigurno, želimo da učenje matematike donosi bogatstvo i radost. Tipičn srednjoškoslki nastavni plan i program engleskog jezika uči đake i gramatici i poeziji. Nastavni plan i program matematike treba da radi isto.
Doduše, ove knjige podrazumevaju da je čitalac – aktuelni nastavnik, budući nastavnik, đak, roditelj, ili bilo ko zainteresovan za matematiku – već imao dodira sa dobrim delom tipičnog školskog programa matematike. Knjige se zasnivaju na toj pretpostavci, a izbor ovakvog pristupa nije bio slučajan iz nekoliko razloga.
1. Dubina ličnog razumevanja samo je rezultat vraćanja na neku priču više puta. Kada se započne sa novom temom, veliki deo mentalnih napora potroši se na razumevanje tehnologije, samih ideja i osećaja za nju. Proces prilagođavanja sopstevnog razmišljanja novim idejam i novim pristupima može biti uzbudljiv, ali i frustrirajući. Međutim, sama činjenica da je neko pročitao na primer, poglavlje o logaritmima, i odradio predviđena vežbanja iz njega, i može da ”uradi” zadatke koji se tiču navedene teme, obično ne znači da je taj neko usvojio temu i stigao do nivoa njenog potpunog razumevanja. Sama dubina teme može se sagledati tek onda kada smo se navikli na topografske odlike njene površine. Kako je jedan od ciljeva ovog teksta da ukaže na dubinu svake od tema koje se izučavaju, moramo biti spremni da je istražimo.
2. Knjiga je napisana sa ciljem da pomogne razvoj i jačanje ličnog razumevanja matematike, ali i da pomogne onima koji su uključeni u proces da prave bolje i opravdane izbore svojih predavačkih metoda i pristupa učenicima. Iako detalji svakog konkretnog nastavnog plana i programa variraju od škole do škole i zavise od udžbenika koji se koristi (pa posledično nije moguće direktno se nasloniti na sve postojeće nastavne planove i programe) izabrali smo da u ovoj ediciji sledimo standardne obimne nastavne teme. Iz tog razloga, ove knjige bi trebalo smatrati nekom vrstom pregleda priča o aritmetici, algebri, funkcijama, integralnom i diferencijalnom računu, verovatnoći, statistici itd. na način na koji su one prikazane u školi.
Ne nudimo savete niti preporuke kako predavati konkretnu temu (uprkos činjenici da se tokom čitanja ovog teksta može izroditi mnoštvo specifičnih nastavnih ideja). Cilj je jednostavno da pomognemo nastavniku ili roditelju da razvije i ojača svoje sopstveno razumevanje, da bude dovoljno obavešten kako bi mogao da donosi lične pedagoške izbore, i da nauči kako da izađe na kraj sa pitanjima koja postavljaju đaci. Učenici koji budu čitali knjige, otkriće dubinu materijala koje su izučavali u školi, ali i dobre naznake kako razmišlja jedan matematičar. Sve u svemu, cilj ove knjige je da poznate koncepte odvede na nove i uzbudljive nivoe.
3. Lako je, relativno lako ”raditi” matematiku. Ali, inovativnost i inicijativa zahtevaju otklon od običnog ”rešavanja” zadataka ka kreativnom i inventivnom. Vodeća kompanija nastoji da pomera granice, da stvara i postavlja nova pitanja, da traga za novim idejama i da pronalazi nove poglede na poznate stvari. Naučno istraživanje deluje sa istim ciljem. Kako se predaje veština postavljanja pitanja? Usmeravnje pažnje na detalje konkretnog nastavnog plana, iako je važno, možda ne pomogne u rešavanju problema opšte perspektive. U ovoj ediciji izabrali smo da naglasimo široke teme kako bismo ilustrovali ”perspektivu” i da ponudimo kontekst i način na koji se mogu istražiti uzbudljivi intelektualni domeni – čak i u okviru nečeg poznatog.
4. Još jedan cilj ove edicije je da jednostavno prikaže mentalni sklop aktivnog matematičara, da ukaže na lepotu matematike, i da omogući uživanje u čistoj radosti istraživanja ovog čudesnog predmeta. Pošto je već iskusio veliki deo standardnog nastavnog programa školske matematike, čitalac poseduje kutiju sa alatom kojim će se igrati. Opremljeni smo za igru!
Zato…, hajde da počnemo sa rešavanjem! Bez obzira na način koji budete izabrali da čitate ovu knjigu – pažljivo čitajući i mozgajući od početka do kraja, ili prelistavajući je i zaustavljajući se na stvarčicama koje vam upadnu u oči – nadam se da ćete imati bogato, intrigantno, prosvetljujuće, korisno i ponajviše radosno iskustvo, jer učenje matematike i bavljenje matematikom upravo treba da bude radosno! Gramatika i poezija u isto vreme.
Autor teksta je Džejms Tenton, poznati matematičar i ovogodišnji gost Maja meseca matematike. Istražite više o Tentonovom gostovanju u Beogradu
